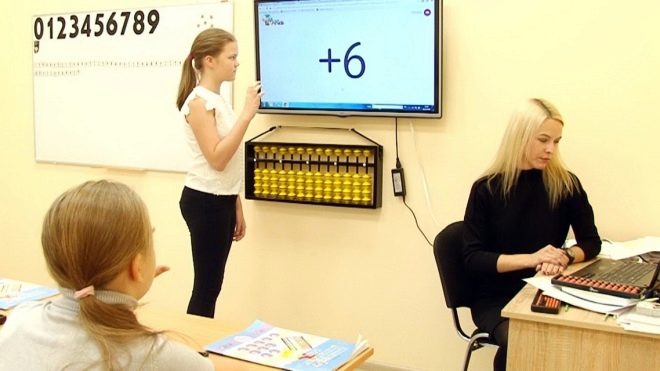How to learn a child to quickly count in your mind?
Parents of modern children with envy are watching the geeks - participants of the television show "Best of All" and "Amazing People" - and worry that their children are not distinguished for their outstanding intelligence and super-wit: they learn poorly the elementary school program, they don’t like to strain their brains and are afraid of lessons mathematics.
From the first class they count on fingers and wands, they do not know oral counting techniques, therefore they have big problems in all subjects of the school course.
The techniques of quick oral counting are simple and easily digested, but it must be remembered that the successful mastery of them implies not mechanical, but quite conscious use of techniques and, in addition, more or less lengthy training.
Having mastered the elementary methods of oral account, using them will be able to correctly and quickly perform instant calculations in the mind with the same accuracy as with written calculations.
Special features
There are so many techniques that promote learning to speed up mental arithmetic. With all the visible differences, they have an important similarity - they are based on three "whales":
- Training and accumulation of experience. Regular practice, the solution of tasks from simple to complex qualitatively and quantitatively change the skill of oral computation.
- Algorithm. Knowledge and application of “secret” methods and laws greatly simplifies the process of counting.
- Abilities and natural endowments. Developed short-term memory and its considerable volume, as well as high concentration of attention - a great help in practicing a quick mental arithmetic. A definite plus is the presence of a mathematical mindset and a predisposition to logical thinking.
The use of the oral account
People are not iron robots, but the fact that they create smart machines speaks of their intellectual superiority. A person needs to constantly keep his brain in good shape, which is actively promoted by the training of skills in mental arithmetic.
For everyday life:
- a successful oral account is an indicator of an analytical mindset;
- regular mental arithmetic will save you from early dementia and senile marasmus;
- your ability to add and subtract well will not allow you to cheat in the store.
For successful study:
- mental activity is activated;
- develop memory, speech, attention, ability to perceive what was said at the hearing, speed of reaction, ingenuity, ability to find the most rational ways to solve the problem;
- strengthened confidence in their capabilities.
When should I start my studies?
According to learned minds (psychologists and educators), a child by the 4th year is already able to add and subtract. By the age of 5, the crumb can freely solve examples and simple tasks. But this is statistics, and children do not always adapt to it. therefore Everything here is purely individual.
In any case, it is better to teach children to count in their minds quickly before they enter school - there will be fewer problems, and a supply of useful skills will help to master modern school programs more successfully.
rules
The Queen of Sciences - Mathematics - took care of the students and made a set of laws, Algorithms and rules, having mastered and skillfully using them, children will love mathematics and mental work:
- The transfer property of addition: swapping the components of the action, we get the same result.
- The combined addition property: when three or more numbers are added together, any two (or more) numerical values can be replaced by their sum.
- Addition and subtraction with the transition through a dozen: add a larger component
- To dozens of round, and then add the remainder of the other component.
- Subtract first the individual units from the number to the sign of the action, and then from the dozens of rounds we subtract the remainder of the deductible.
- Having presented the diminished in the form of the sum of tens and units, we remove from the tens of the larger the smaller and add to the answer the units of the diminishing.
- When adding and subtracting dozens of rounds (they are still called “round” numbers), dozens can be considered the same as units.
- Addition and subtraction of tens and units. Dozens more convenient to add to the tens, and units - to units.
Adding a number to the sum
The methods are as follows:
- We calculate its value, and then add this value to it.
- We add it to the first term, and then we add the second term to the result.
- We add the number to the second term, and then add the first term to the answer.
The addition of the amount to the number
The methods are as follows:
- We calculate its testimony, and then we add to the number.
- We add the first term to the number, and then we add the second term to the result.
- We add the second term to the number, and then we add the first term to the result.
The addition of two sums. Adding two sums, we choose the most convenient way to calculate.
Using the main multiplication properties
The techniques are as follows:
- The transfer property of multiplication. If we change the factors in places, their product will not change.
- The combined property of multiplication. When multiplying three or more numbers, any two (or more) numbers can be replaced by their product.
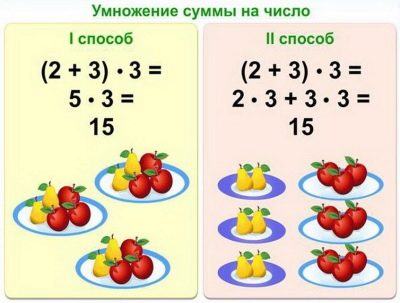
- Distribution property of multiplication. To multiply the sum by a number, it is necessary to multiply each of its components by this number and add the resulting works.
Multiply and divide numbers by 10 and 100
Ways:
- To increase any number by 10 times, you must add one zero to the right.
- In order to do this 100 times, two zeros must be assigned to it on the right.
- To reduce the number by 10 times, you need to drop one zero to the right, and to divide by 100 - two zeros.
Multiply the amount by the number
Ways:
- 1st method. Calculate the amount and multiply it by this value.
- 2nd way. Multiply the number with each of the addends, and add the received answers.
Multiply number by sum
Ways:
- 1st method. Find the sum and multiply the number of what we get.
- 2nd way. Multiply the number by each of the addends, and add the resulting works.
Dividing the amount by the number
Ways:
- 1st method. Calculate the amount and divide it by a number.
- 2nd way. Each of the addends is divided by the number and the resulting quotients are added.
Dividing the number of the product
Options:
- 1st method. Divide the number by the first factor, and then divide the result by the second factor.
- 2nd way. Divide the number by the second factor, and then divide the result by the first factor.
Kinds
At the lessons on the oral account scanty time is given, but this does not detract from its importance for the development of children's mental activity. Verbal computational skills are formed in the mathematics lessons in elementary school when performing various types of tasks and exercises.
Find the value of a math expression
These can be ordinary numeric expressions or expressions with a variable (alphabetic), and numeric values are suggested for letters.Substituting numbers instead of letters, find the numerical value of the resulting expression.
Compare Math Expressions
Such tasks are varied:
- determine the equality or inequality of these two expressions (after finding and comparing their values);
- to the relation given to the sign and one of the expressions to compose the second expression or to complete the unfinished proposed one
- in such exercises, single-digit, two-digit, three-digit numbers and quantities can be used in expressions and all four arithmetic operations. The main purpose of such tasks is a solid assimilation of theoretical material and the development of computational skills.
- Solve the equations. They help to understand the connections between components and the results of arithmetic operations.
- To solve a task. It can be both simple and complex tasks. With their help, theoretical knowledge is strengthened, computational skills and skills are developed, children's mental activity is activated.
Oral account receptions
Signs of divisibility of numbers:
- by 2: all that exceed it, and in the numerical row go through one;
- on 3 and 9: if the sum of the digits is a multiple of these indicators without a balance;
- by 4: if the last two digits in the record successively form a number that is divided by 4;
- 5: round dozens and those where there is 5 at the end;
- by 6: numbers that are multiples of two and three are divided;
- 10: numeric values, in which the record is at the end is 0;
- 12: divide the numbers that can be divided into three and four at the same time;
- by 15: numbers that are divided at the same time into single-valued integral components of this number factors.
Primary school account forms
It is well known that the main activity of preschoolers and younger students is a game that is useful to include in all stages of the lesson. Some forms of the oral account will be given below.
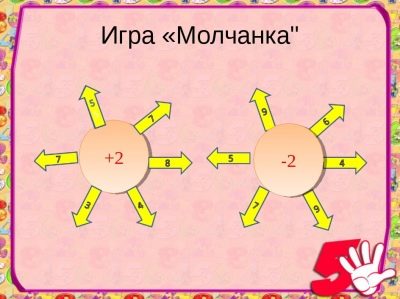
The game "Silent"
It helps to cultivate attention and discipline. A silence can consist of examples in one action, two or more. It is played in all classes of elementary school with both abstract integers and named numbers.
The students consider in their minds and silently on call, the teachers write the answers to the examples offered to them on the blackboard. The correct answers are met with light claps, and the wrong answers with silence.
Game "Lotto"
There may be several types corresponding to those sections of mathematics that are studied and need to be fixed. For example, lotto with examples of multiplication and division within the "hundreds".
To give more interest to the game, tires with answers can be made from a cut picture. If all the examples are solved correctly, a picture is made from the tires.
Game "Arithmetic labyrinths"
They look like concentric circles with gates with numbers. To get to the center, you need to dial a number in the center. Labyrinths for the decision can demand either one action (addition), or several. It should be noted that these tasks have several solutions.
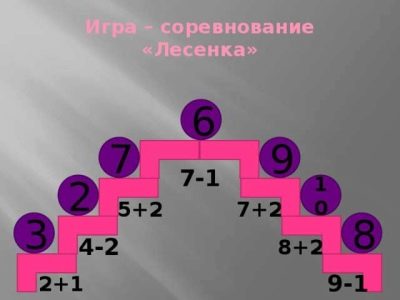
The game "Catch the pilot" (a kind of "ladder")
On the drawing board: a plane with loops, in which examples. Two summoned students record responses to the left and right of the loops. Who correctly and quickly decides, he will catch up with the pilot.
The game "Circular Examples"
Didactic material is a set of cards, arranged in envelopes; Each of them has 8 cards, each of which contains one example.
The numerical examples in each envelope are different in their content and are selected according to the principle of self-control: when resolving them, the result of one example will be the beginning of the next.
Circular examples may be offered as ladders.
Methods and techniques of development
Considering the ways to teach children of 6 years to quick counting in their mind, it is impossible not to note the uniqueness and simplicity of the Japanese method of counting “Soroban”. The Soroban technique allows you to train children aged 4 to 11 years, developing their mental abilities and expanding the range of intellectual abilities of children.It is easy to teach any student to take examples of math in the mind, using the Japanese method of counting on sorobane. By practicing mental verbal counts, we put the whole brain into operation., thereby unloading the left hemisphere, which is responsible for solving mathematical problems.
Mental arithmetic allows even the “figurative” hemisphere to be interested in computational operations, which increases the efficiency of the brain.
Large numbers require written methods of calculation, although there are individuals who hone their skills in working with them.
Considering examples of mathematics in the mind is a vital necessity, since the exams at school are now without the use of calculators, and the ability to count in the mind is included in the list of mandatory skills of graduates of 9 and 11 grades.
The basic rule for mental addition is:
- If the first term is a two-digit number (not a round dozen), then add 9 to it as follows: add 10, remove 1.
- Add 8: add 10, remove 2.
Quickly add two-digit numbers:
- If the last digit of the second term is greater than 5, round it upwards. We perform the addition, from the resulting amount we remove the "additive".
- If the last digit of the second term is less than 5, then add up by digits: first, add dozens, then - units.
- You can swap the terms in places, but add the numbers using the same algorithm.
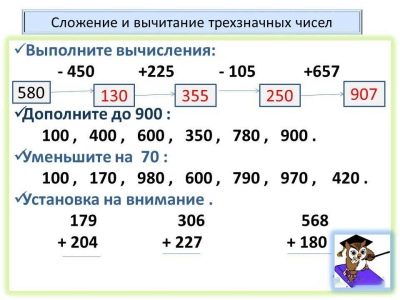
Subtraction features: reduction to round numbers
Unambiguous deductible is rounded up to 10, two-digit - up to 100. Subtract 10 or 100 and add the amendment. Reception is relevant for small amendments.
Subtract three-digit numbers in mind
Based on a good knowledge of the composition of the numbers of the first ten, you can subtract in parts in this order: hundreds, tens, units.
Multiply and divide can be easily, knowing the multiplication table - “magic wand” to the rapid development of the account in mind. It is noteworthy that the village children of pre-revolutionary Russia knew the continuation of the so-called Pythagorean table - from 11 to 19, and it would be nice for modern scholars to know the table up to 19 * 9 by heart.
The most interesting tricks
To captivate children with mathematics and make the difficult moments in the school curriculum closer and more accessible, there are ways and methods, Turning difficulties into fun and interesting:
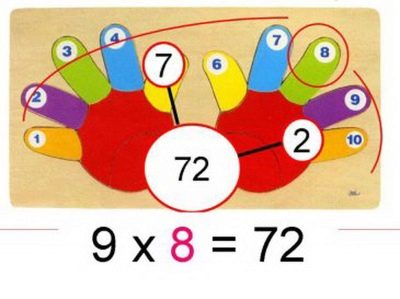
- To multiply any single digit by 9, let’s show everyone our empty palms. Bend your finger, corresponding in order (counting from the thumb of the left hand) to the number of the first factor. We look at how many fingers to the left of the bent - it will be dozens of the desired work, and to the right - his own unit.
- Multiplication by 11 of any two-digit number, the sum of which does not reach 10, is fun and simple: mentally move the digits of this number and put their sum between them - the answer is ready.
- If the sum of digits multiplied by 11 turns out to be 10 or more than 10, then between the mentally spaced digits of this number you should put their sum and add the first two digits to the left, leaving the other two unchanged, to get the product.
For information on how to teach your child to instantly count in your mind, see the following video.